Continuous Time Bayesian Networks

This paper describes a new way of modeling the changes in a state space over time called Continuous Time Bayesian Networks (CTBNs). It uses a novel graphical model framework which competes with a Dynamic Bayesian Network and is specifically trying to move away from methods which require high frequency discrete updates to "simulate" continuous time. It also attempts to address the correlation problem which Koller describes as the entanglement problem, an effect in DBNs which causes independent random variables to have a dependency due to frequent updates. At the core of this technique are homogenous Markov processes (HMP) which look like a particular interpretation of Markov Models: The transitions in a Markov process correspond to temporal changes. The transition probabilities do not change over time and are therefore "homogenous". Every state has a self-transition and therefore the distribution over staying in a state is exponential. Instead of a conditional probability table, there is a "conditional intensity matrix" (CIM) which describes the exponential transitions between states.

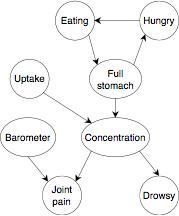
A CTBN factors the state space much like a Bayesian influence diagram. The image above shows the graphical model which describes the independencies in a particular domain related to drug response. In the CTBN paradigm, cycles are allowed. This is due to the fact that all influence is considered to occur over time however infinitesimal that amount of time may be. So, for example, in the diagram on the left, the cycle at the top of the diagram would be interpreted from a DBN perspective as Eating_N -> FullStomach_N+dt , FullStomach_N -> Hungry_N+dt , and Hungry_N -> Eating_N+dt. Because the influences are factored, each influence arrow A->B has a different CIM for each joint setting of the parents of A.

One of the best motivations for creating this paradigm is because in one calculation it is possible to exactly infer the distribution over the state of the HMP without higher frequency updates. So given a distribution over the state at time T, the distribution over the state at time T+s can be calculated directly in one step regardless of the value of s. This answers one of my questions about how reasoning could be done more efficiently than a DBN which I raised in my review of A Closed-Form Solution for Mapping General Distributions to Minimal PH Distributions

Another question I had about this technique was: What happens if you query the state of the system at a very large time in the future? The authors confirmed my suspicion that the distribution always tends toward the "prior" which in this case is called the "stationary distribution."

The first approximate inference algorithm that was proposed for CTBNs, the "Linearization Method", basically assumed that the exponential distributions were linear and that the values of the random variables didn't change between updates. This is funny because it basically means that this inference method is only valid over short time intervals, exactly the problem that CTBNs were supposed to improve over DBNs! The second inference algorithm, the "Sub-System Method", seemed inconsistent. Sometimes it worked well in the short-term and sometimes it worked better in the long-term. All of the approximate methods did better with frequent updates, whether artificially induced or due to the presence of observations.

So my conclusion is that this is a step in the right direction because it explicitly models continuous time. I like the elegance of the method and the possibility of modeling more complicated distributions than exponentials through combinations of exponentials. I think it's premature though to say that it is clearly a better approach than DBNs. It certainly appeals to a mathematical sense of being the "right" way to reason about time in a Bayesian model, but the experiments don't seem to conclude that CTBNs have fixed the problems that DBNs have.