November 17, 2004
Modeling ADLs with Untimed HMMs: updated
|
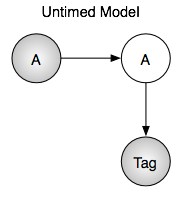
There are now four models that I have tested with this data. The first model is a simple HMM that is event driven: activities are only allowed to switch when a tag is seen. This is called the "Untimed" Model. |
|
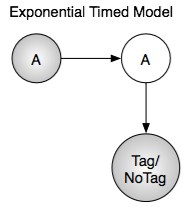
In the first three cases to model this domain with HMMs I segmented each of the traces into their 12 composite activities. I calculated P(RFID objects given activity). In the timed cases I added a null observation for each second in which there was no RFID observation. Then I constructed an HMM in which there was one node for each activity. Each node has a self-transition whose probability was calculated based on mean duration (exponential timed case) or mean number of observations per activity (untimed case). In the gamma case the "D"uration varable governs the "A"ctivity state switches. Each "A"ctivity state can transition to any of the other 13 states with a uniform probability. The HMMs start with a uniform prior over all of the activities. I then performed 17 fold cross-validation on the user traces and determined the viterbi path through the state space that corresponded to left out user trace. |
|
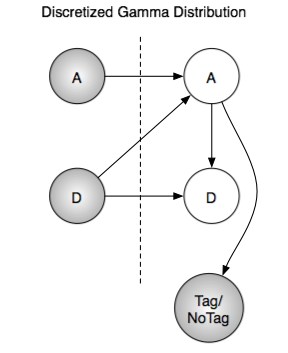
For the gamma distribution I used the DBN on the left to do inference. Since I'm using a plain vanilla viterbi algorithm I create the full |A|x|D| state space to represent the world. "A" is the Activity that is being performed. "D" is the number of seconds left in the activity. Normally "A" stays the same from time to time+1, and "D" counts down deterministically. When "D" reaches 0, "A" is chosen uniformly from the next possible activities. Then "D" is chosen according the gamma distribution associated with the new "A". Then I do exact inference to explain the observed tag sequence and recover the optimal state path through time. |
|
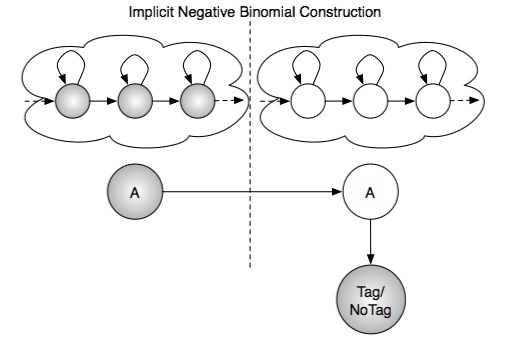
For the fourth system I enforced each activity to consist of a three state sequence which was trained using EM. |
Here are some comparitive results for using flavors of HMMs to recognize ADLs. In both cases the same data set was used: The dataset that Matthai first recorded at his house.
Info about the dataset
| Activity Class | # of traces in dataset | Duration of Activity (sec.) | Average # of objects touched | |
| 1 | Personal Appearance | 16 | 91 | 5.13 |
| 2 | Oral Hygiene | 13 | 108 | 6.38 |
| 3 | Toileting | 15 | 111 | 4.67 |
| 4 | Hand Washing | 11 | 75 | 3.82 |
| 5 | Housecleaning | 16 | 134 | 3.69 |
| 6 | Appliance Usage | 13(or 16 depending) | 92 | 3.15 |
| 7 | Prepare a snack | 12 | 174 | 7.75 |
| 8 | Prepare a drink | 19(or 16 depending) | 135 | 4.84 |
| 9 | Control the temperature | 15 | 67 | 1.13 |
| 10 | Laundry | 11 | 146 | 4.36 |
| 11 | Leisure | 15 | 152 | 3.47 |
| 12 | Telephone Usage | 17 | 149 | 3.00 |
| 13 | Infant Care | 17 | 160 | 5.94 |
| 14 | Take Medication | 14 | 74 | 2.5 |
| Mean (std) | 14.6 (2.4) | 119(35) | 4.27 (1.7) | |
Info about the results
| Untimed HMM | Timed HMM | Discrete Gamma | Implicit Gamma | ||
| Total Number of Activities user's performed: | (17*12) = 204 | ||||
| Number of completely missed Activities (False Negatives) | 7 | 18 | 14 | 9 | |
| * | Average duration of missed activity (sec) | 71.0 | 76.7 | 70.07 | 82 |
| * | Average number of objects touched in a missed activity | 2.0 | 2.3 | 2.2 | 3.4 |
| Number of added Activities (False Positives) | 32 | 6 | 8 | 40 | |
| Number of confused Activities | 9 | 14 | 14 | 13 | |
| Total errors FP+FN+Confused | 49 | 38 | 36 | 62 | |
| Overall Recall (Correctly guessed activities)/(All true activities) | 191/204=93.6% | 172/204=84.3% | 176/204=86.3% | 182/204=89.2% | |
| Overall Precision (Correctly guessed activiites)/(All guessed activities) | 191/229 =83.4% | 172/192= 89.6% | 176/198= 88.9% | 182/235=77.4% | |
Confusion Matrix for HMM without timing
| Guess-> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | FN |
| 1 | 14 | 1 | 1 | ||||||||||||
| 2 | 13 | ||||||||||||||
| 3 | 14 | 1 | |||||||||||||
| 4 | 1 | 8 | 2 | ||||||||||||
| 5 | 16 | ||||||||||||||
| 6 | 11 | 2 | |||||||||||||
| 7 | 12 | ||||||||||||||
| 8 | 1 | 14 | 1 | 3 | |||||||||||
| 9 | 15 | ||||||||||||||
| 10 | 11 | ||||||||||||||
| 11 | 15 | ||||||||||||||
| 12 | 17 | ||||||||||||||
| 13 | 17 | ||||||||||||||
| 14 | 14 | ||||||||||||||
| FP | 0 | 2 | 4 | 2 | 3 | 7 | 3 | 6 | 0 | 3 | 2 | 0 | 0 | 0 | |
Confusion Matrix for HMM with exponential timing
| Guess-> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | FN |
| 1 | 11 | 1 | 2 | 2 | |||||||||||
| 2 | 13 | ||||||||||||||
| 3 | 7 | 7 | 1 | ||||||||||||
| 4 | 1 | 8 | 2 | ||||||||||||
| 5 | 15 | 1 | |||||||||||||
| 6 | 14 | 1 | 1 | ||||||||||||
| 7 | 12 | ||||||||||||||
| 8 | 1 | 8 | 7 | ||||||||||||
| 9 | 13 | 2 | |||||||||||||
| 10 | 10 | 1 | |||||||||||||
| 11 | 13 | 2 | |||||||||||||
| 12 | 17 | ||||||||||||||
| 13 | 17 | ||||||||||||||
| 14 | 14 | ||||||||||||||
| FP | 0 | 2 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Confusion Matrix for HMM with discretized gamma function
| Guess-> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | FN |
| 1 | 14 | 2 | 0 | ||||||||||||
| 2 | 13 | ||||||||||||||
| 3 | 8 | 6 | 1 | ||||||||||||
| 4 | 1 | 8 | 2 | ||||||||||||
| 5 | 15 | 1 | |||||||||||||
| 6 | 13 | 1 | 1 | 1 | |||||||||||
| 7 | 12 | ||||||||||||||
| 8 | 1 | 1 | 8 | 6 | |||||||||||
| 9 | 1 | 14 | 0 | ||||||||||||
| 10 | 11 | 0 | |||||||||||||
| 11 | 12 | 3 | |||||||||||||
| 12 | 17 | ||||||||||||||
| 13 | 17 | ||||||||||||||
| 14 | 14 | ||||||||||||||
| FP | 0 | 2 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |
Confusion Matrix for HMM with implicit gamma function
| Guess-> | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | FN |
| 1 | 13 | 3 | 0 | ||||||||||||
| 2 | 13 | ||||||||||||||
| 3 | 11 | 2 | 1 | 1 | |||||||||||
| 4 | 2 | 6 | 3 | ||||||||||||
| 5 | 1 | 13 | 1 | 1 | |||||||||||
| 6 | 12 | 1 | 1 | ||||||||||||
| 7 | 12 | ||||||||||||||
| 8 | 13 | 1 | 1 | 2 | |||||||||||
| 9 | 15 | 0 | |||||||||||||
| 10 | 11 | 0 | |||||||||||||
| 11 | 15 | 0 | |||||||||||||
| 12 | 17 | ||||||||||||||
| 13 | 17 | ||||||||||||||
| 14 | 14 | ||||||||||||||
| FP | 5 | 1 | 1 | 3 | 8 | 4 | 4 | 2 | 1 | 6 | 2 | 0 | 0 | 3 | |

