What is #P (sharp-P) complexity?

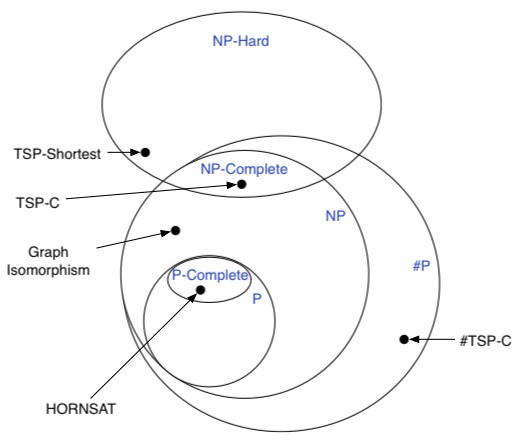
Above is a diagram of my view of some complexity results.

P is the set of problems that are solvable in polynomial time.

P-Complete is the set of problems which all problems in P can be polynomial-time reduced to which are also in P. HORNSAT is an example of a problem in P-complete. It is the problem of finding a satisfying assignment to a set of Horn Clauses.

NP is the class of problems for which a solution can be guessed or verified in polynomial time. It may or may not be larger than the set P (P = NP?). NP-Hard problems are problems that all problems in NP can be polynomial time reduced to. NP-Complete problems are problems which are both NP-Hard and in NP. NP-Hard problems aren't necessarily in NP. Graph-isomorphism is the problem of determining if there is a node-to-node and edge-to-edge mapping of one graph to another. It is an example of an NP problem which is not NP-complete. TSP-C (Travelling Salesman Problem) is the problem of determining a sequence of all vertices on a graph, which have edges connecting them in sequence whose sum is less than C. Finding such a path is an NP-Complete problem.

Finding the shortest TSP path, TSP-shortest, is NP-Hard and is harder than NP because verifying the shortest path is harder than a polynomial time check.

#P (sharp-P) is the problem of finding the number of solutions to a problem in NP. It is strictly harder than NP, but the relationship between #P and NP-Hard is not clear.