State Machine for 591RL

Here is the state machine that I like:

Parameter Estimation

There is a progression of sophistication in parameter estimation which goes as follows, from less sophisticated to more sophisticate:

• Maximum Likelihood:
  This is a point estimate of a parameter which defines an unobservable distribution. It is obtained by choosing the parameter of a function which maximizes the likelihood that the function will generate the observed data. It is a bad estimate in the case of sparse data.
  In practice the maximum likelihood parameter is found by solving the first derivative of the likelihood function analytically and finding the setting of the parameter that causes the derivative to go to 0. (With some assumption about the likelihood function, I suppose)
• Maxium a Posteriori Estimate:
  This is also a point estimate of a distribution. But this technique is less-biased in the presence of sparse data because it assumes that there is a prior distribution over the parameters which is known and taken into account when estimating the parameterization of the likelihood function.
• Bayesian Esimation:
  This is an estimation technique which estimates a distribution over the parameter. It is not a point estimate of the parameter. It assumes a prior distribution and produces a posterior distribution of the likelihood function parameter.

Evaluation of timing distributions

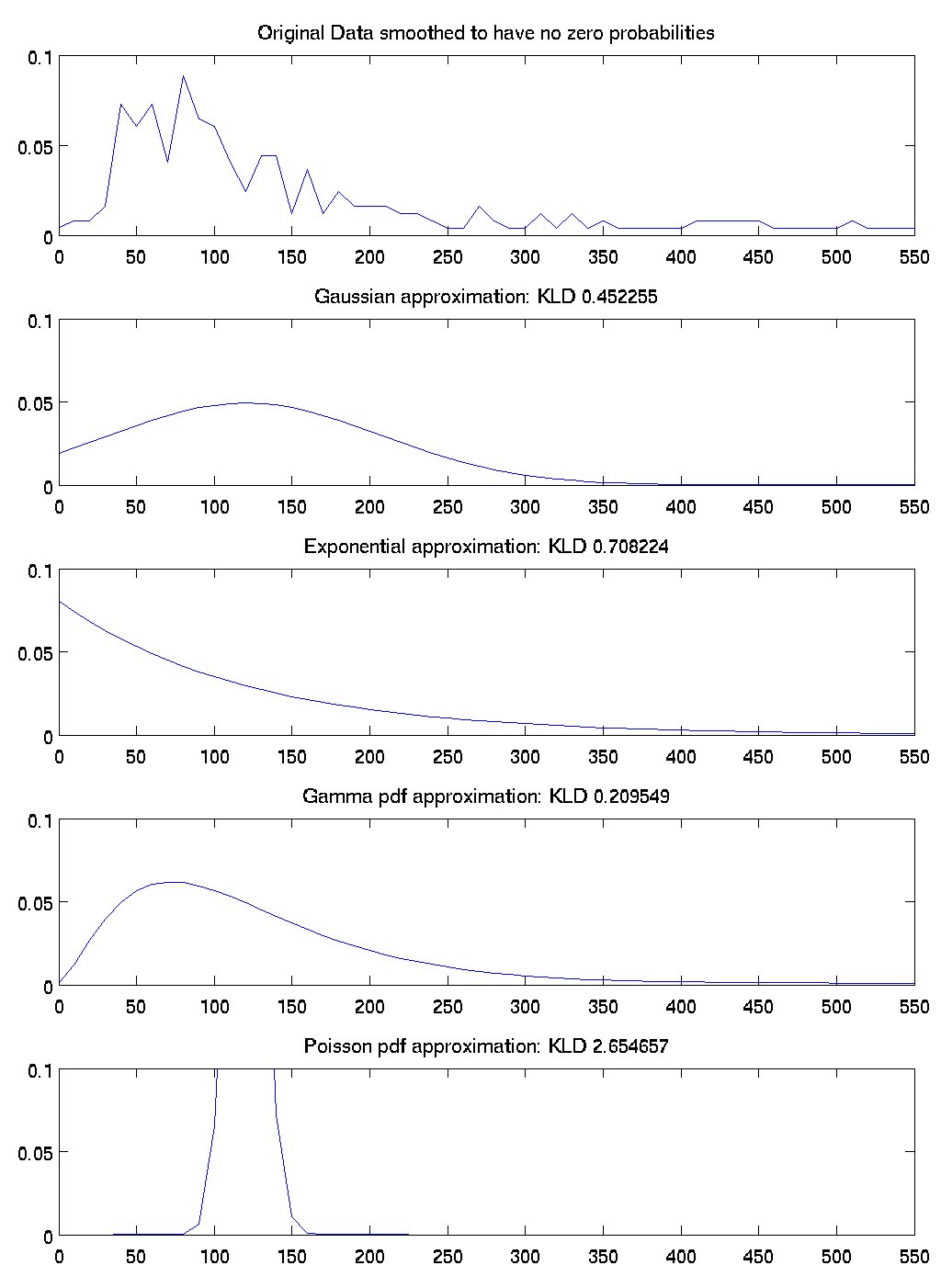
Here is some data that shows how well four different distributions match the true timing distribution in the data. To get these numbers, I took all the activities that were in the ADL dataset from Matthai's house and I ignored which activity generated them. I then generated a histogram of the activity durations. That is the first graph.

The subsequent graphs show a gaussian approximation with the same mean and std as the original data, an exponential approximation with the same mean as the original data, the maximum likelihood gamma-pdf approximation of the data, and an approximation of a Poisson distribution that matches the original data. For each of these graphs I calculated the KLD divergence of the approximation with the original data. According to KLD measures, the best fits were, in order, gamma, gaussian, exponential, and poisson.

So this justifies the choice of the gamma-pdf distribution for activity times, at least among these four options.

Conjugate Priors

A conjugate prior is a distribution whose aposterior estimate has the same form as the prior. This is good because it allows arbitrary numbers of updates to be made to the distribution as more data becomes available.