What is #P (sharp-P) complexity?

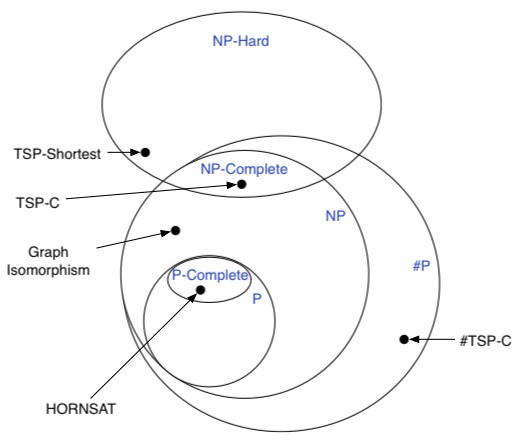
Above is a diagram of my view of some complexity results.

P is the set of problems that are solvable in polynomial time.

P-Complete is the set of problems which all problems in P can be polynomial-time reduced to which are also in P. HORNSAT is an example of a problem in P-complete. It is the problem of finding a satisfying assignment to a set of Horn Clauses.

NP is the class of problems for which a solution can be guessed or verified in polynomial time. It may or may not be larger than the set P (P = NP?). NP-Hard problems are problems that all problems in NP can be polynomial time reduced to. NP-Complete problems are problems which are both NP-Hard and in NP. NP-Hard problems aren't necessarily in NP. Graph-isomorphism is the problem of determining if there is a node-to-node and edge-to-edge mapping of one graph to another. It is an example of an NP problem which is not NP-complete. TSP-C (Travelling Salesman Problem) is the problem of determining a sequence of all vertices on a graph, which have edges connecting them in sequence whose sum is less than C. Finding such a path is an NP-Complete problem.

Finding the shortest TSP path, TSP-shortest, is NP-Hard and is harder than NP because verifying the shortest path is harder than a polynomial time check.

#P (sharp-P) is the problem of finding the number of solutions to a problem in NP. It is strictly harder than NP, but the relationship between #P and NP-Hard is not clear.

What is a Horn clause?

A Horn clause is restricted to have at most one positive literal. They are typically written as an implication statement which can be converted to a disjunctive clause:

Horn clauses are an interesting restriction because they allow efficient resolution and are the basis of the language Prolog.

See MathWorld for more.

What is the difference between Generative and Discriminative Learning?

Generally speaking in generative learning one is trying to optimize the parameters of a generative model to best explain the data that is observed. In discriminative learning there is no model assumed, but instead a function is optimized to best discriminate among classes. In the second case no assumption is made about the underlying process which is generating the data.

Generative	Discriminative
Maximize P(C,A1,...,AN)	Maximize P(C | A1,...,AN)
Example: Naive Bayes	Example: Logistic Regression
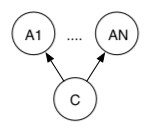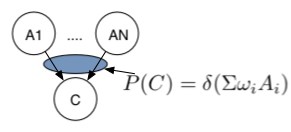	A Bayes Net with a restricted CPT
Learning is just a matter of counting the training data.	Learning takes more work and is an optimization procedure